Tung Độ Gốc là gì? Cách Tính Hệ Số Gốc Đường Thẳng Có Lời Giải
Tung độ gốc là gì? Cách để Tính hệ số góc, tung và hoành độ gốc của đường thẳng, ví dụ, đồ thị hàm số, lời giải, đáp án, các hỏi đáp từ A-Z.
Trong toán học, đặc biệt là đại số và hình học giải tích, việc xác định các yếu tố quan trọng của một đường thẳng như hệ số góc, tung độ gốc và hoành độ gốc là vô cùng cần thiết.

Tung Độ Gốc là gì? Cách Tính Hệ Số Gốc Đường Thẳng Có Lời Giải
Những giá trị này không chỉ giúp chúng ta vẽ chính xác đồ thị hàm số mà còn hỗ trợ trong việc phân tích, dự đoán xu hướng trong nhiều lĩnh vực như vật lý, tài chính và khoa học dữ liệu.
Vậy tung độ gốc là gì? Làm sao để tính hệ số góc, xác định tung độ gốc và hoành độ gốc một cách chính xác?
20 ý Tưởng Sáng Tạo Độc Lạ
Trong bài viết này, chúng ta sẽ cùng tìm hiểu chi tiết về các khái niệm trên, đi kèm ví dụ minh họa, đồ thị trực quan, các câu hỏi – đáp phổ biến và lời giải chi tiết cho từng bài toán cụ thể.
Hãy cùng khám phá toàn bộ kiến thức từ A-Z về chủ đề này để có thể áp dụng một cách hiệu quả vào học tập và thực tế!
Tung độ gốc là gì?
Tung độ gốc là giá trị của tung độ (y) tại điểm mà đường thẳng cắt trục tung (Oy) trong hệ tọa độ Oxy.
Tung độ gốc trong các loại hàm số khác nhau:
- Hàm bậc hai: y=ax2+bx+cy = ax^2 + bx + cy=ax2+bx+c, tung độ gốc là ccc.
- Hàm số mũ: y=ax+by = a^x + by=ax+b, tung độ gốc là 1+b1 + b1+b (khi x=0x = 0x=0).
- Hàm số logarit: y=loga(x)+by = \log_a(x) + by=loga(x)+b, tung độ gốc là bbb (nếu xác định được khi x=1x = 1x=1).
Tung độ gốc trong thực tế:
- Trong vật lý, nếu một phương trình biểu diễn sự chuyển động s=vt+s0s = vt + s_0s=vt+s0, thì tung độ gốc s0s_0s0 là vị trí ban đầu.
- Trong kinh tế, nếu một hàm số biểu diễn lợi nhuận P=ax+bP = ax + bP=ax+b, thì tung độ gốc bbb có thể là lợi nhuận ban đầu khi chưa bán được sản phẩm nào.
Mối quan hệ với hệ số góc
- Tung độ gốc bbb giúp xác định điểm xuất phát trên trục OyOyOy, trong khi hệ số góc aaa thể hiện độ dốc của đường thẳng.
- Hai yếu tố này quyết định vị trí và hướng của đường thẳng trong hệ tọa độ.
Cơ Hội Thách Thức Sinh Viên
Tung độ gốc là một khái niệm cơ bản nhưng quan trọng trong toán học, giúp ta hiểu rõ hơn về đồ thị của hàm số và mối quan hệ giữa các biến số.

Tung độ gốc là gì?
Cách tính hệ số độ góc tung và hoành của đường thẳng
Bạn đang muốn tìm hiểu cách tính hệ số góc, tung độ gốc, và hoành độ gốc của đường thẳng?
20 ý Tưởng Sáng Tạo Độc Lạ
Dưới đây là cách tính chi tiết từng yếu tố này:
1. Hệ số góc (a):
- Hệ số góc của đường thẳng là đại lượng biểu thị độ dốc của đường thẳng đó.
- Nó cho biết đường thẳng đó nghiêng bao nhiêu so với trục hoành.
Cách tính:
Nếu đường thẳng có phương trình dạng y = ax + b, thì a chính là hệ số góc.
Nếu biết hai điểm (x1, y1) và (x2, y2) nằm trên đường thẳng, hệ số góc được tính bằng công thức:
a = (y2 – y1) / (x2 – x1)
Nếu biết góc α tạo bởi đường thẳng và trục Ox thì hệ số góc được tính theo công thức: a = tan(α)
2. Tung độ gốc (b):
Tung độ gốc là giá trị của y khi x = 0.
Nói cách khác, đó là điểm mà đường thẳng cắt trục tung (trục Oy).
Cách tính:
- Nếu đường thẳng có phương trình dạng y = ax + b, thì b chính là tung độ gốc.
- Nếu biết 1 điểm (x,y) nằm trên đường thẳng và biết hệ số góc a thì ta có thể tính b theo công thức: b = y-ax.
3. Hoành độ gốc:
Hoành độ gốc là giá trị của x khi y = 0.
Nói cách khác, đó là điểm mà đường thẳng cắt trục hoành (trục Ox).
Cách tính:
- Nếu đường thẳng có phương trình dạng y = ax + b, để tìm hoành độ gốc ta cho y = 0 và giải phương trình để tìm x. khi đó x = -b/a.
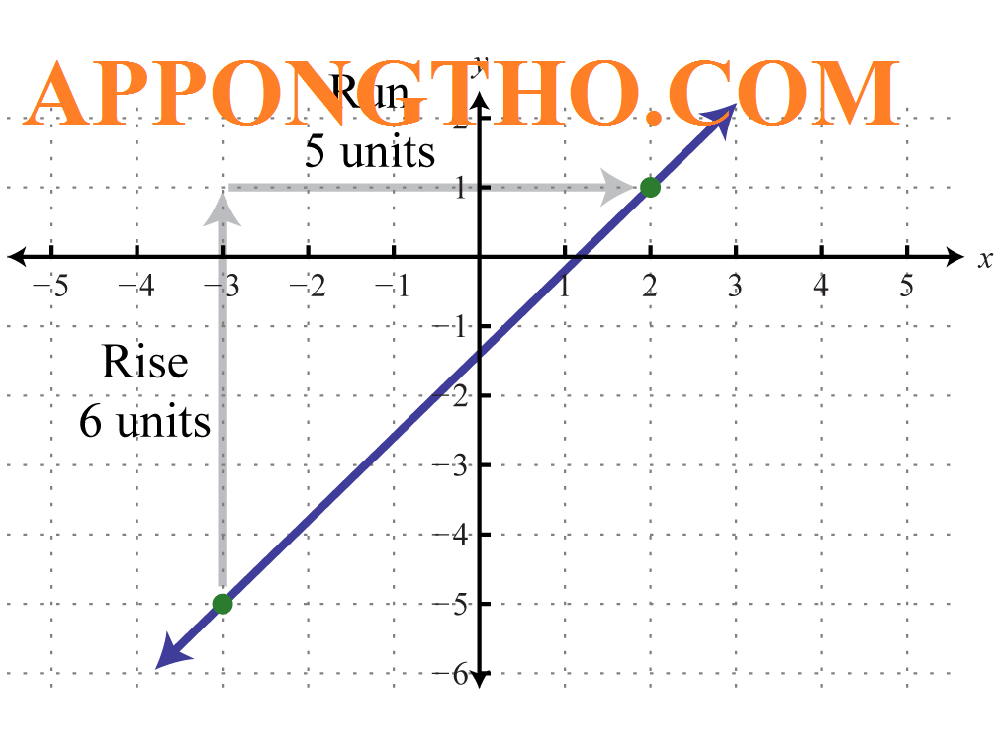
Bài tập đại số ví dụ tung độ góc
Bài tập đại số ví dụ tung độ góc
Dưới đây là 5 bài tập khác nhau về tung độ gốc, mỗi bài tập đều có ví dụ, giải thích, đáp án chi tiết và kết luận:
Bài tập 1: Tìm tung độ gốc từ phương trình đường thẳng
Đề bài: Cho các phương trình đường thẳng sau, hãy xác định tung độ gốc của mỗi đường thẳng:
- a) y = 4x + 7
- b) y = -2x + 3
- c) y = x – 5
- d) y = -0.5x + 1.5
- e) y = 6
Giải thích:
- Tung độ gốc là giá trị của y khi x = 0.
- Trong phương trình đường thẳng dạng y = ax + b, tung độ gốc chính là b.
Đáp án:
- a) Tung độ gốc: 7
- b) Tung độ gốc: 3
- c) Tung độ gốc: -5
- d) Tung độ gốc: 1.5
- e) Tung độ gốc: 6
Bài Tập Về Âm Tiết Tiếng Việt
Việc xác định nhanh chóng tung độ gốc từ phương trình giúp ta dễ dàng hình dung vị trí đường thẳng cắt trục tung, hỗ trợ vẽ đồ thị và giải quyết các bài toán liên quan.
Bài tập 2: Xác định tung độ gốc từ đồ thị
Đề bài: Cho đồ thị của các đường thẳng trên hệ tọa độ Oxy, hãy xác định tung độ gốc của mỗi đường thẳng.
Giải thích:
- Tung độ gốc là điểm mà đường thẳng cắt trục tung (trục Oy).
- Tìm điểm giao của đường thẳng với trục Oy, giá trị y của điểm đó chính là tung độ gốc.
Đáp án:
Để trả lời chính xác câu hỏi này, bạn cần cung cấp một đồ thị có sẳn các đường thẳng trên hệ trục Oxy.
- Nhưng tôi có thể hướng dẫn bạn cách xác định:
- Tìm điểm mà đường thẳng cắt trục tung.
- Đọc giá trị y của điểm đó.
- Giá trị y đó chính là tung độ gốc.
Phẩm chất 4 kỹ thuật khác nhau để học sinh hiểu
Đồ thị hóa phương trình đường thẳng giúp trực quan hóa tung độ gốc, cho phép ta hiểu rõ hơn về mối quan hệ giữa các biến số và ứng dụng trong thực tế.

Xác định tung độ gốc từ đồ thị
Bài tập 3: Tìm phương trình đường thẳng khi biết tung độ gốc và hệ số góc
Đề bài: Tìm phương trình đường thẳng khi biết:
- a) Hệ số góc là 2 và tung độ gốc là 3.
- b) Hệ số góc là -1 và tung độ gốc là -4.
Giải thích:
- Phương trình đường thẳng có dạng y = ax + b, trong đó a là hệ số góc và b là tung độ gốc.
- Thay các giá trị đã cho vào phương trình để tìm phương trình đường thẳng.
Đáp án:
- a) y = 2x + 3
- b) y = -x – 4
Tung độ gốc và hệ số góc là hai yếu tố then chốt để xác định duy nhất một đường thẳng trên mặt phẳng tọa độ.
Giáo Án Trò Chơi Mèo Đuổi Chuột
Hiểu rõ mối quan hệ này giúp ta viết phương trình đường thẳng một cách chính xác.
Bài tập 4: Ứng dụng tung độ gốc trong bài toán thực tế
Đề bài: Một chiếc xe ô tô bắt đầu di chuyển từ vị trí cách điểm xuất phát 5km. Vận tốc của xe là 60km/h. Hãy viết phương trình biểu diễn quãng đường đi được của xe theo thời gian và xác định tung độ gốc.
Giải thích:
- Quãng đường đi được (y) phụ thuộc vào thời gian (x) và vận tốc.
- Phương trình có dạng y = ax + b, trong đó a là vận tốc và b là quãng đường ban đầu.
Đáp án:
- Phương trình: y = 60x + 5
- Tung độ gốc: 5 (biểu thị quãng đường ban đầu là 5km)
Trong các bài toán thực tế, tung độ gốc thường biểu thị giá trị ban đầu của một đại lượng nào đó.
Bài Tập Lập Bảng Cân Đối Kế Toán
Việc hiểu rõ ý nghĩa của tung độ gốc giúp ta mô hình hóa và giải quyết các vấn đề một cách hiệu quả.
Bài tập 5: Tìm tung độ gốc khi biết 2 điểm thuộc đường thẳng.
Đề bài: Tìm tung độ gốc của đường thẳng đi qua 2 điểm A(1,5) và B(2,8).
Giải thích:
- Đầu tiên ta tính hệ số góc của đường thẳng. a = (y2-y1)/(x2-x1).
- Sau đó ta thay 1 trong 2 điểm và hệ số góc vừa tìm được vào phương trình đường thẳng y = ax + b để tìm b (tung độ gốc).
Đáp án:
- Hệ số góc của đường thẳng là: a = (8-5)/(2-1) = 3.
- Thay điểm A(1,5) vào phương trình ta có: 5 = 3*1 + b => b = 2.
- Vậy tung độ gốc của đường thẳng là 2.
100 Số Mang Ý Nghĩa Mật Mã Tình Yêu Của Giới Trẻ
Việc tính toán được hệ số góc và tung độ gốc khi biết 2 điểm thuộc đường thẳng, cho phép ta biết được phương trình đường thẳng đó, từ đó có thể ứng dụng vào việc giải những bài toán liên quan đến các điểm nằm trên đường thẳng đó.

Đồ thị hàm số tung độ góc
Đồ thị hàm số tung độ góc
Trong toán học, đồ thị của một hàm số bậc nhất có dạng:
y=ax+by = ax + by=ax+b
Trong đó:
- aaa: Hệ số góc (độ dốc của đường thẳng).
- bbb: Tung độ gốc, tức là giá trị của yyy khi x=0x = 0x=0.
Đoạn Văn how to stay healthy
Đây là điểm mà đồ thị cắt trục tung (trục OyOyOy).
1. Cách xác định tung độ gốc trên đồ thị
- Trên trục tọa độ, tung độ gốc bbb là điểm mà đường thẳng cắt trục tung (trục OyOyOy, tức là khi x=0x = 0x=0).
- Điểm này có tọa độ (0,b)(0, b)(0,b).
- Nếu b>0b > 0b>0, đường thẳng cắt trục tung phía trên gốc tọa độ.
- Nếu b<0b < 0b<0, đường thẳng cắt trục tung phía dưới gốc tọa độ.
- Nếu b=0b = 0b=0, đường thẳng đi qua gốc tọa độ (0,0)(0,0)(0,0).
2. Ví dụ đồ thị với các giá trị khác nhau của tung độ gốc
Ví dụ 1: y=2x+3y = 2x + 3y=2x+3
- Hệ số góc a=2a = 2a=2 (đường thẳng dốc lên).
- Tung độ gốc b=3b = 3b=3, tức là đường thẳng cắt trục tung tại (0,3)(0,3)(0,3).
- Khi x=0x = 0x=0, y=3y = 3y=3, nghĩa là đường thẳng đi qua điểm (0,3)(0,3)(0,3).
Ví dụ 2: y=−x+5y = -x + 5y=−x+5
- Hệ số góc a=−1a = -1a=−1 (đường thẳng dốc xuống).
- Tung độ gốc b=5b = 5b=5, tức là đường thẳng cắt trục tung tại (0,5)(0,5)(0,5).
Ví dụ 3: y=3x−2y = 3x – 2y=3x−2
- Hệ số góc a=3a = 3a=3.
- Tung độ gốc b=−2b = -2b=−2, nghĩa là đường thẳng cắt trục tung tại (0,−2)(0,-2)(0,−2).
Until Now Thì Là Gì? 15 Lỗi Thường Gặp Khi Sử Dụng Until
3. Vẽ đồ thị hàm số với tung độ gốc
Để vẽ đồ thị một đường thẳng y = ax + b, ta thực hiện các bước sau:
- Xác định tung độ gốc bbb: Chấm điểm (0,b)(0, b)(0,b) trên trục tung.
- Chọn một giá trị bất kỳ của xxx và tính yyy.
- Nối hai điểm vừa tìm được để tạo thành đường thẳng.
- Kéo dài đường thẳng về hai phía để hoàn thành đồ thị.
-

(FAQ) hỏi đáp về tung độ gốc
(FAQ) hỏi đáp về tung độ gốc
Dưới đây là 28 câu hỏi quan đến tung độ gốc, được giải đáp, có thể bạn đang cần:
1. Xác định tung độ gốc trên đồ thị?
Tung độ gốc là điểm mà đồ thị cắt trục tung (Oy), giúp xác định vị trí bắt đầu của đường thẳng trên hệ trục tọa độ.
- Điểm trên trục tung khi x=0x = 0x=0.
- Tìm bằng cách thay x=0x = 0x=0 vào phương trình đường thẳng.
- Nếu phương trình là y=ax+by = ax + by=ax+b, thì tung độ gốc là bbb.
- Đánh dấu điểm (0,b)(0, b)(0,b) trên đồ thị.
- Đường thẳng luôn đi qua điểm đó.
- Xác định thêm một điểm khác để vẽ đường thẳng chính xác.
Địa Chỉ Mua Bán Sách Cũ
Tung độ gốc là thông tin quan trọng giúp vẽ và phân tích đồ thị hàm số một cách nhanh chóng.
2. Phương trình đường thẳng khi tung độ gốc bằng 0?
Khi tung độ gốc bằng 0, phương trình đường thẳng đi qua gốc tọa độ, có dạng đơn giản hơn.
- Phương trình có dạng y=axy = axy=ax.
- Đường thẳng đi qua điểm (0,0)(0,0)(0,0).
- Hệ số góc aaa quyết định độ nghiêng.
- Nếu a=0a = 0a=0, đường thẳng trùng trục hoành.
- Nếu a>0a > 0a>0, đường thẳng dốc lên.
- Nếu a<0a < 0a<0, đường thẳng dốc xuống.
Phương trình này thể hiện mối quan hệ tuyến tính trực tiếp mà không có thành phần dịch chuyển theo trục tung.
3. Tung độ gốc liên quan gì đến hệ số góc?
Tung độ gốc và hệ số góc là hai tham số quan trọng trong phương trình đường thẳng, quyết định vị trí và độ dốc của nó.
- Hệ số góc aaa xác định độ dốc.
- Tung độ gốc bbb xác định điểm cắt trục tung.
- Nếu bbb thay đổi, đường thẳng tịnh tiến theo trục tung.
- Nếu aaa thay đổi, độ dốc của đường thẳng thay đổi.
- Hai đường có cùng aaa nhưng khác bbb là song song.
- Nếu b=0b = 0b=0, đường thẳng đi qua gốc tọa độ.
20 Ứng Dụng Học Tiếng Trung Quốc
Sự kết hợp giữa hệ số góc và tung độ gốc giúp mô tả chính xác đường thẳng trong hệ tọa độ.
4. Tính tung độ gốc khi biết hai điểm?
Tung độ gốc có thể được xác định khi biết hai điểm trên đường thẳng, giúp viết phương trình chính xác.
- Gọi hai điểm là (x1,y1)(x_1, y_1)(x1,y1) và (x2,y2)(x_2, y_2)(x2,y2).
- Tính hệ số góc: a=y2−y1x2−x1a = \frac{y_2 – y_1}{x_2 – x_1}a=x2−x1y2−y1.
- Dùng phương trình đường thẳng y=ax+by = ax + by=ax+b.
- Thay một điểm bất kỳ vào phương trình để tìm bbb.
- Giải phương trình để xác định tung độ gốc.
- Xác minh lại bằng cách kiểm tra điểm còn lại.
Việc tính tung độ gốc từ hai điểm giúp xác định chính xác vị trí cắt trục tung của đường thẳng.
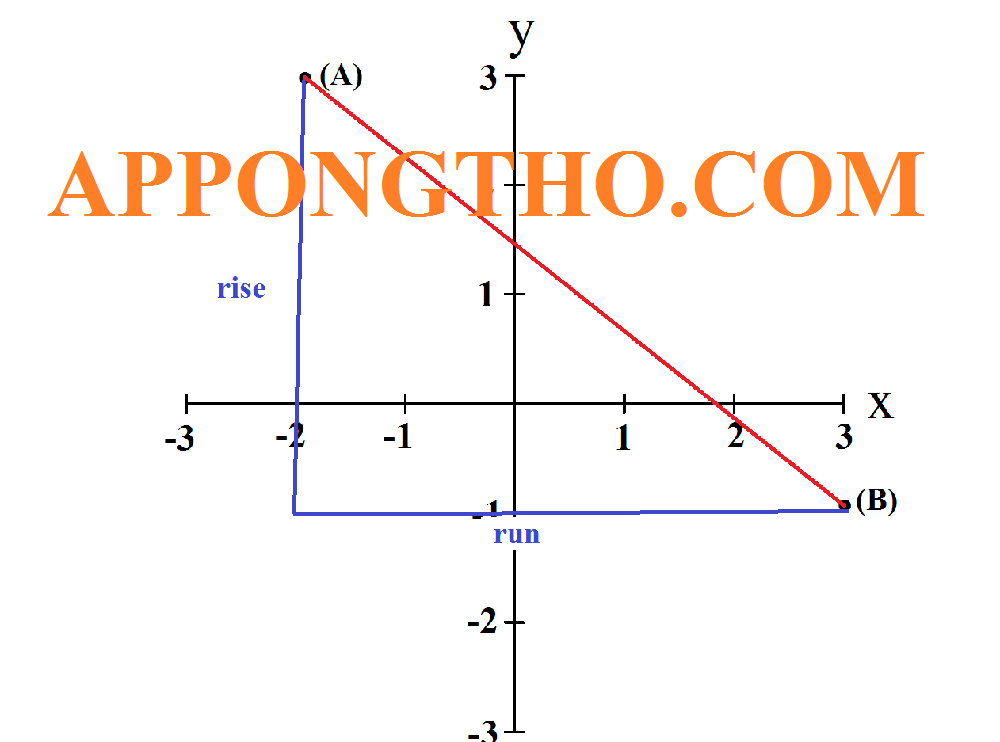
Ý nghĩa tung độ gốc trong thực tế?
5. Ý nghĩa tung độ gốc trong thực tế?
Tung độ gốc có ứng dụng thực tế quan trọng trong nhiều lĩnh vực như tài chính, vật lý, kinh tế và kỹ thuật.
- Trong tài chính, nó là giá trị ban đầu khi không có đầu vào.
- Trong vật lý, nó có thể là vị trí ban đầu của một vật chuyển động.
- Trong kinh tế, nó thể hiện giá trị cố định khi biến số khác bằng 0.
- Trong kỹ thuật, nó xác định mức cơ bản của một hệ thống.
- Trong thống kê, nó giúp dự báo xu hướng dữ liệu.
- Trong đồ thị học, nó là điểm khởi đầu của đường biểu diễn.
Công Thức Tính Hệ Số Nở Rời Của Đất
Nhờ ý nghĩa quan trọng này, tung độ gốc giúp phân tích và dự đoán xu hướng một cách chính xác hơn.
6. Tung độ gốc khác gì hoành độ gốc?
Mặc dù đều liên quan đến vị trí cắt trục tọa độ, nhưng tung độ gốc và hoành độ gốc khác nhau về vai trò và ý nghĩa.
- Tung độ gốc là giá trị yyy khi x=0x = 0x=0.
- Hoành độ gốc là giá trị xxx khi y=0y = 0y=0.
- Tung độ gốc xác định điểm cắt trục tung.
- Hoành độ gốc xác định điểm cắt trục hoành.
- Tung độ gốc là hệ số tự do trong phương trình bậc nhất.
- Hoành độ gốc phụ thuộc vào hệ số góc và tung độ gốc.
Hai khái niệm này bổ trợ lẫn nhau giúp xác định chính xác đặc điểm của đường thẳng trên hệ tọa độ.
7. Tìm tung độ gốc từ phương trình?
Tung độ gốc có thể được xác định dễ dàng từ phương trình đường thẳng, giúp xác định điểm cắt trục tung.
- Phương trình có dạng y=ax+by = ax + by=ax+b.
- Tung độ gốc chính là bbb.
- Nếu phương trình dạng tổng quát Ax+By+C=0Ax + By + C = 0Ax+By+C=0, ta chuyển về dạng y=−ABx−CBy = -\frac{A}{B}x – \frac{C}{B}y=−BAx−BC.
- Khi đó, b=−CBb = -\frac{C}{B}b=−BC.
- Nếu C=0C = 0C=0, đường thẳng đi qua gốc tọa độ.
- Nếu B=0B = 0B=0, đường thẳng song song với trục tung, không xác định tung độ gốc.
Mở Design Ideas Trong Powerpoint
Xác định tung độ gốc từ phương trình giúp nhanh chóng phân tích đồ thị và đặc điểm của đường thẳng.
8. Tung độ gốc đường thẳng song song trục hoành?
Khi một đường thẳng song song với trục hoành, tung độ gốc của nó có đặc điểm đặc biệt và dễ nhận biết.
- Phương trình dạng y=by = by=b.
- Hệ số góc a=0a = 0a=0.
- Đường thẳng đi qua mọi điểm có tung độ bằng bbb.
- Không thay đổi dù hoành độ khác nhau.
- Luôn cắt trục tung tại điểm (0,b)(0, b)(0,b).
- Không có hoành độ gốc vì không cắt trục hoành.
Đường thẳng song song trục hoành có tung độ gốc chính là giá trị cố định của hàm số.
9. Tung độ gốc có thể âm không?
Tung độ gốc có thể nhận giá trị âm, thể hiện vị trí cắt trục tung nằm dưới trục hoành.
- Nếu b<0b < 0b<0, đường thẳng cắt trục tung dưới gốc tọa độ.
- Khi a>0a > 0a>0, đường thẳng đi lên từ điểm âm đó.
- Khi a<0a < 0a<0, đường thẳng đi xuống từ điểm âm đó.
- Dữ liệu thực tế như lỗ tài chính có thể có tung độ gốc âm.
- Trong vật lý, vị trí dưới mốc quy ước có thể có giá trị âm.
- Nếu tung độ gốc âm, giá trị yyy ban đầu là nhỏ hơn 0.
Đọc Sơ Đồ Tải Của Cẩu Nhanh
Tung độ gốc âm là điều hoàn toàn bình thường và có thể gặp trong nhiều bài toán thực tế.
Tung độ gốc có thể bằng 0 không?
10. Tung độ gốc có thể bằng 0 không?
Khi tung độ gốc bằng 0, đường thẳng đi qua gốc tọa độ và có một số tính chất đặc biệt.
- Phương trình có dạng y=axy = axy=ax.
- Đi qua điểm (0,0)(0,0)(0,0).
- Nếu a>0a > 0a>0, đường thẳng đi lên từ gốc.
- Nếu a<0a < 0a<0, đường thẳng đi xuống từ gốc.
- Không có phần bù trừ trong giá trị yyy.
- Chỉ phụ thuộc vào hệ số góc aaa.
Tung độ gốc bằng 0 cho thấy đường thẳng bắt đầu từ gốc tọa độ mà không có sự dịch chuyển theo trục tung.
11. Tung độ gốc có thể dương không?
Tung độ gốc có thể dương, biểu thị rằng đường thẳng cắt trục tung tại điểm phía trên trục hoành.
- Nếu b>0b > 0b>0, đường thẳng cắt trục tung ở điểm (0,b)(0, b)(0,b).
- Khi a>0a > 0a>0, đường thẳng dốc lên từ điểm đó.
- Khi a<0a < 0a<0, đường thẳng dốc xuống từ điểm đó.
- Giá trị bbb càng lớn, điểm cắt càng cao.
- Trong thực tế, số dư tài chính có thể biểu thị bằng tung độ gốc dương.
- Trong vật lý, vị trí trên mốc quy ước có thể có tung độ gốc dương.
Ứng Dụng Tự Học Tiếng Hàn Quốc
Tung độ gốc dương thể hiện giá trị khởi điểm cao hơn gốc tọa độ trong hệ trục tọa độ Descartes.
12. Tung độ gốc có thể là phân số không?
Tung độ gốc hoàn toàn có thể là một phân số, đặc biệt khi dữ liệu không phải số nguyên.
- Nếu phương trình có dạng y=ax+mny = ax + \frac{m}{n}y=ax+nm.
- Điểm cắt trục tung sẽ là (0,mn)(0, \frac{m}{n})(0,nm).
- Số phân số thường xuất hiện trong các bài toán tỷ lệ.
- Trong thống kê, trung bình của dữ liệu có thể là phân số.
- Trong vật lý, các đơn vị đo lường có thể dẫn đến tung độ gốc phân số.
- Trong tài chính, giá trị khởi điểm có thể ở dạng phân số.
Việc có tung độ gốc là phân số giúp mô tả chính xác hơn các đại lượng liên tục trong thực tế.
13. Tung độ gốc có thể là số vô tỉ không?
Tung độ gốc có thể là một số vô tỉ, đặc biệt khi phương trình xuất hiện hằng số đặc biệt như π\piπ hoặc 2\sqrt{2}2.
- Ví dụ: phương trình y=ax+πy = ax + \piy=ax+π.
- Điểm cắt trục tung là (0,π)(0, \pi)(0,π).
- Một số hằng số tự nhiên có thể tạo tung độ gốc vô tỉ.
- Trong lượng giác, các phương trình có thể chứa π\piπ.
- Trong vật lý, các hằng số tự nhiên có thể là số vô tỉ.
- Trong toán học thuần túy, nghiệm của một số phương trình có thể là số vô tỉ.
Vẽ Sơ Đồ Phả Hệ Trong Word
Sự xuất hiện của số vô tỉ làm tăng tính chính xác và ý nghĩa toán học của tung độ gốc trong một số trường hợp.
14. Tung độ gốc có thể là số thập phân không?
Tung độ gốc có thể là một số thập phân, thường thấy trong các ứng dụng thực tế.
- Nếu phương trình có dạng y=ax+2.5y = ax + 2.5y=ax+2.5.
- Điểm cắt trục tung là (0,2.5)(0, 2.5)(0,2.5).
- Số thập phân xuất hiện khi đơn vị đo lường không nguyên.
- Trong tài chính, giá trị tiền tệ có thể chứa số thập phân.
- Trong khoa học, số đo có thể có dạng thập phân.
- Trong thống kê, trung bình cộng thường là số thập phân.
Tung độ gốc dạng thập phân giúp tăng độ chính xác trong các tính toán thực tế.
15. Tung độ gốc có thể là biến số không?
Tung độ gốc có thể là một biến số trong trường hợp phương trình không cố định.
- Nếu phương trình có dạng y=ax+b(x)y = ax + b(x)y=ax+b(x).
- Giá trị b(x)b(x)b(x) có thể thay đổi theo biến số khác.
- Trong bài toán tối ưu hóa, tung độ gốc có thể thay đổi.
- Trong thống kê, giá trị tung độ gốc có thể phụ thuộc vào biến độc lập.
- Trong kinh tế, chi phí ban đầu có thể biến đổi theo thời gian.
- Trong vật lý, mốc năng lượng ban đầu có thể phụ thuộc vào điều kiện ban đầu.
Sao Chép Sơ Đồ Trong Word
Sự xuất hiện của biến số trong tung độ gốc tạo ra các mô hình linh hoạt hơn trong toán học và thực tế.
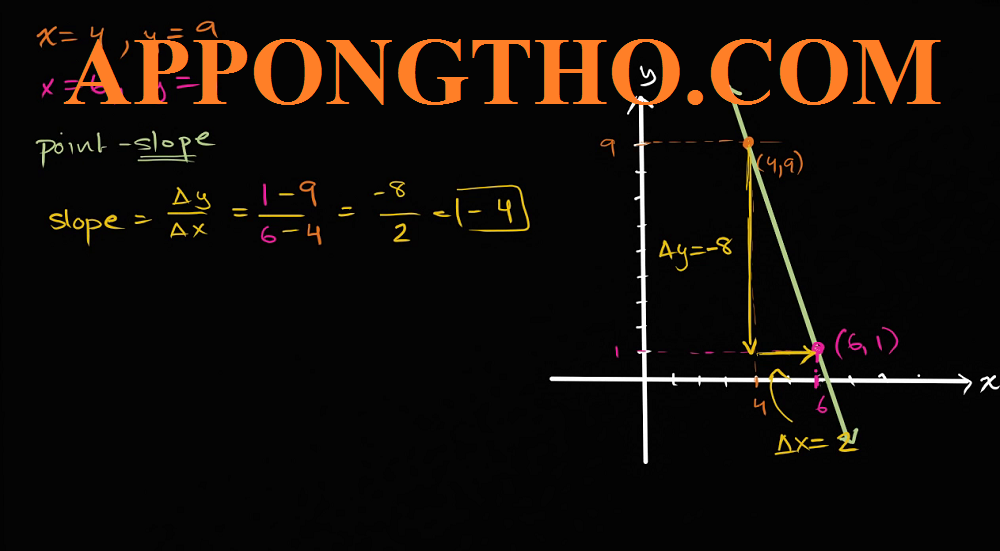
Tung độ gốc có thay đổi không?
16. Tung độ gốc có thể là hằng số không?
Tung độ gốc luôn là một hằng số nếu phương trình tuyến tính cố định.
- Nếu phương trình có dạng y=ax+by = ax + by=ax+b, thì bbb là hằng số.
- Điểm cắt trục tung không thay đổi.
- Nếu bbb thay đổi, đó là một phương trình khác.
- Trong các mô hình tuyến tính, bbb là giá trị không đổi.
- Trong đồ thị học, điểm cắt trục tung cố định.
- Trong tài chính, số dư ban đầu thường là hằng số.
Giá vốn hàng bán tăng
Khi tung độ gốc là hằng số, nó giúp xác định chính xác vị trí ban đầu trên đồ thị.
17. Tung độ gốc có thay đổi không?
Tung độ gốc không thay đổi trong một phương trình tuyến tính cố định nhưng có thể thay đổi khi điều kiện thay đổi.
- Nếu phương trình cố định, bbb là không đổi.
- Nếu phương trình thay đổi, bbb có thể thay đổi theo điều kiện.
- Trong thực tế, chi phí ban đầu có thể thay đổi theo thời gian.
- Trong khoa học, điều kiện môi trường có thể làm thay đổi giá trị ban đầu.
- Trong tài chính, vốn đầu tư ban đầu có thể thay đổi.
- Trong kinh tế, lạm phát có thể làm thay đổi giá trị gốc.
Tung độ gốc có thể thay đổi khi mô hình hoặc điều kiện ban đầu thay đổi, nhưng trong một phương trình cụ thể, nó là cố định.
18. Tung độ gốc liên quan gì đến điểm cắt trục tung?
Tung độ gốc chính là điểm mà đường thẳng cắt trục tung trên đồ thị.
- Nếu phương trình có dạng y=ax+by = ax + by=ax+b, thì điểm cắt là (0,b)(0, b)(0,b).
- Điểm này luôn nằm trên trục tung.
- Xác định điểm này giúp vẽ đồ thị chính xác.
- Trong thực tế, đó là giá trị ban đầu của một hệ thống.
- Đóng vai trò quan trọng trong phân tích dữ liệu.
- Giúp xác định xu hướng chung của hàm số.
Định Luật Pascal
Tung độ gốc và điểm cắt trục tung là hai khái niệm đồng nhất trong đồ thị hàm số.
19. Tung độ gốc liên quan gì đến gốc tọa độ?
Tung độ gốc thể hiện mối quan hệ của đường thẳng với gốc tọa độ.
- Nếu tung độ gốc bằng 0, đường thẳng đi qua gốc tọa độ (0,0)(0,0)(0,0).
- Nếu b>0b > 0b>0, đường thẳng cắt trục tung trên gốc tọa độ.
- Nếu b<0b < 0b<0, đường thẳng cắt trục tung dưới gốc tọa độ.
- Gốc tọa độ là điểm tham chiếu quan trọng trong phân tích đồ thị.
- Trong vật lý, gốc tọa độ là vị trí ban đầu của một vật.
- Trong tài chính, gốc tọa độ có thể là thời điểm khởi đầu của một khoản đầu tư.
Tung độ gốc giúp xác định khoảng cách từ đường thẳng đến gốc tọa độ trong hệ trục tọa độ Descartes.
20. Tung độ gốc liên quan gì đến phương trình bậc nhất?
Tung độ gốc là một thành phần quan trọng trong phương trình bậc nhất.
- Phương trình bậc nhất có dạng y=ax+by = ax + by=ax+b.
- Tung độ gốc chính là hệ số tự do bbb.
- Nếu b=0b = 0b=0, đường thẳng đi qua gốc tọa độ.
- Nếu b≠0b \neq 0b=0, đường thẳng cắt trục tung tại (0,b)(0, b)(0,b).
- Giá trị này không ảnh hưởng đến hệ số góc.
- Dễ dàng xác định bằng cách cho x=0x = 0x=0.
Sơ Đồ Tư Duy Vật Lý 9 Chương 2 Điện Từ Học
Tung độ gốc đóng vai trò quan trọng trong việc xác định đặc điểm đồ thị của phương trình bậc nhất.
21. Tung độ gốc liên quan gì đến hàm số bậc hai?
Tung độ gốc là hệ số tự do trong phương trình hàm số bậc hai.
- Hàm số bậc hai có dạng y=ax2+bx+cy = ax^2 + bx + cy=ax2+bx+c.
- Tung độ gốc là giá trị ccc, tức là điểm cắt trục tung (0,c)(0, c)(0,c).
- Nếu c=0c = 0c=0, đồ thị đi qua gốc tọa độ.
- Ảnh hưởng của tung độ gốc nhỏ hơn hệ số aaa và bbb đối với hình dạng đồ thị.
- Xác định nhanh bằng cách cho x=0x = 0x=0.
- Trong thực tế, nó có thể đại diện cho giá trị ban đầu của một hệ thống phi tuyến.
Tung độ gốc giúp xác định điểm xuất phát của đồ thị hàm số bậc hai trên trục tung.
22. Tung độ gốc có ảnh hưởng gì đến độ dốc của đồ thị?
Tung độ gốc không ảnh hưởng đến độ dốc nhưng ảnh hưởng đến vị trí của đường thẳng.
- Độ dốc của đường thẳng chỉ phụ thuộc vào hệ số góc aaa.
- Tung độ gốc bbb chỉ quyết định vị trí đường thẳng trên trục tung.
- Nếu tăng bbb, đường thẳng tịnh tiến lên trên.
- Nếu giảm bbb, đường thẳng tịnh tiến xuống dưới.
- Trong thực tế, nó quyết định mức khởi điểm của một xu hướng.
- Không ảnh hưởng đến sự thay đổi của yyy theo xxx.
Vẽ Sơ Đồ Pert Có Lời Giải
Tung độ gốc chỉ dịch chuyển đồ thị mà không thay đổi độ dốc của nó.
23. Tung độ gốc có vai trò gì trong thực tế?
Tung độ gốc có nhiều ứng dụng trong các lĩnh vực thực tế khác nhau:
- Kinh tế: Chi phí cố định trong mô hình chi phí tổng.
- Khoa học: Giá trị ban đầu của một phản ứng hóa học.
- Vật lý: Vị trí ban đầu của một vật trong chuyển động.
- Tài chính: Số dư ban đầu của một tài khoản ngân hàng.
- Thống kê: Điểm xuất phát của một xu hướng dữ liệu.
- Công nghệ: Mức điện áp ban đầu trong một mạch điện.
Tung độ gốc là một giá trị quan trọng trong việc xác định điểm xuất phát của nhiều hệ thống khác nhau.
24. Làm thế nào để tính tung độ gốc từ bảng dữ liệu?
Để tính tung độ gốc từ bảng dữ liệu, bạn có thể thực hiện các bước sau:
- Chọn hai điểm bất kỳ (x1,y1)(x_1, y_1)(x1,y1) và (x2,y2)(x_2, y_2)(x2,y2).
- Tính hệ số góc bằng công thức a=y2−y1x2−x1a = \frac{y_2 – y_1}{x_2 – x_1}a=x2−x1y2−y1.
- Dùng phương trình đường thẳng: y=ax+by = ax + by=ax+b.
Thay tọa độ một điểm vào phương trình:
- Chọn một điểm (x1,y1)(x_1, y_1)(x1,y1).
- Giải phương trình y1=ax1+by_1 = ax_1 + by1=ax1+b để tìm bbb.
Kết luận: Giá trị bbb là tung độ gốc.
NPV Là Gì? 10 Bài Tập Tính NPV Của Dự Án
Phương pháp này giúp tìm tung độ gốc từ dữ liệu thực nghiệm một cách chính xác.
25. Có công thức nào xác định tung độ gốc không?
Có công thức chung để xác định tung độ gốc từ phương trình đường thẳng:
- Nếu phương trình có dạng y=ax+by = ax + by=ax+b, thì bbb chính là tung độ gốc.
- Nếu biết hệ số góc aaa và một điểm (x,y)(x, y)(x,y), dùng công thức: b=y−axb = y – axb=y−ax
Nếu có hai điểm (x1,y1)(x_1, y_1)(x1,y1) và (x2,y2)(x_2, y_2)(x2,y2), dùng công thức:
- a=y2−y1x2−x1a = \frac{y_2 – y_1}{x_2 – x_1}a=x2−x1y2−y1.
- b=y1−ax1b = y_1 – ax_1b=y1−ax1.
Công thức này giúp xác định chính xác tung độ gốc từ dữ liệu thực tế.
26. Tung độ gốc có ảnh hưởng gì đến đồ thị của phương trình?
Tung độ gốc quyết định vị trí cắt trục tung của đồ thị.
- Nếu b>0b > 0b>0, đồ thị cắt trục tung phía trên gốc tọa độ.
- Nếu b<0b < 0b<0, đồ thị cắt trục tung phía dưới gốc tọa độ.
- Nếu b=0b = 0b=0, đồ thị đi qua gốc tọa độ.
- Giá trị lớn hơn của bbb làm đồ thị tịnh tiến lên trên.
- Giá trị nhỏ hơn của bbb làm đồ thị tịnh tiến xuống dưới.
- Không ảnh hưởng đến độ dốc của đường thẳng.
Năng Lượng Nghỉ Là Gì? Khối Năng Lượng Nghỉ Và Toàn Phần
Tung độ gốc giúp định vị chính xác đường thẳng trên hệ trục tọa độ.
27. Tung độ gốc có ứng dụng gì trong kinh tế?
Trong kinh tế, tung độ gốc thường xuất hiện trong nhiều mô hình:
- Chi phí cố định: Mô hình chi phí có dạng C=ax+bC = ax + bC=ax+b, với bbb là chi phí ban đầu.
- Doanh thu ban đầu: Một doanh nghiệp có thể có doanh thu ban đầu mà không cần bán sản phẩm.
- Mô hình cung cầu: Trong một số trường hợp, giá trị ban đầu có thể là một giá trị cố định.
- Lãi suất ngân hàng: Tiền lãi ban đầu có thể được coi là một dạng tung độ gốc.
- Đầu tư: Giá trị tài sản ban đầu trong một khoản đầu tư.
Tung độ gốc giúp phân tích và dự đoán các yếu tố kinh tế quan trọng.
Hiểu rõ về tung độ gốc, hoành độ gốc và hệ số góc không chỉ giúp chúng ta giải quyết các bài toán liên quan đến phương trình đường thẳng mà còn mở rộng ứng dụng vào thực tế, từ mô hình tài chính đến phân tích dữ liệu.
pH và pKa là gì? Hiểu mối quan hệ giữa pH và pKa
Qua bài viết này, bạn đã nắm được cách xác định những thông số quan trọng này, biết cách vẽ đồ thị chính xác và giải các bài toán thực tế một cách khoa học.
Với những ví dụ cụ thể, lời giải chi tiết và hệ thống câu hỏi từ A-Z, bạn hoàn toàn có thể tự tin áp dụng kiến thức này vào các bài tập cũng như trong những lĩnh vực nghiên cứu khác nhau.
Hãy tiếp tục rèn luyện, thực hành và khám phá thêm để nắm vững các nguyên tắc quan trọng của hình học giải tích và đại số! 🚀








