Nguyên lý xếp chồng là gì? Phương pháp, Ứng dụng, nguyên lý xếp chồng mạch điện, dòng điện vòng, điện thế, định lý, nguồn dòng tác động.
Trong khoa học kỹ thuật và vật lý hiện đại, việc phân tích và giải các hệ thống phức tạp luôn đòi hỏi những phương pháp tối ưu giúp đơn giản hóa bài toán nhưng vẫn đảm bảo độ chính xác cao.
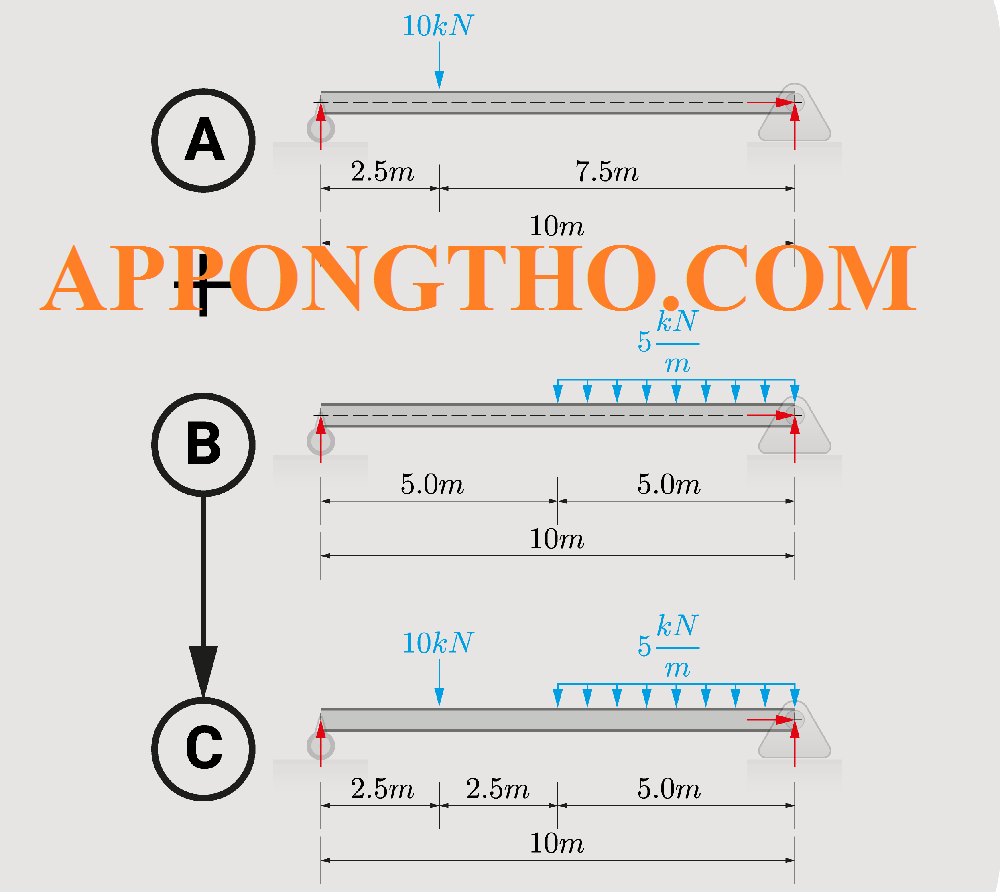
Nguyên Lý Xếp Chồng Mạch Điện, Dòng Điện, Ứng Dụng
Một trong những nguyên lý cơ bản và được ứng dụng rộng rãi nhất trong lĩnh vực này là nguyên lý xếp chồng (hay còn gọi là nguyên lý chồng chất).
Nguyên lý này đặc biệt quan trọng trong các hệ tuyến tính, cho phép tách riêng từng tác động của các nguồn lực, nguồn điện hoặc nguồn dòng, từ đó tổng hợp lại để tìm ra đáp ứng tổng thể của hệ thống.
Trong lĩnh vực mạch điện, nguyên lý xếp chồng giúp chúng ta tính toán nhanh chóng dòng điện, điện áp trong mạch có nhiều nguồn tác động bằng cách phân tích từng nguồn một cách riêng rẽ.
Ngoài ra, nguyên lý này còn liên quan mật thiết đến các khái niệm quan trọng như dòng điện vòng, điện thế nút, các định lý tương đương mạch như Thevenin, Norton và ảnh hưởng của nguồn dòng khi tác động riêng lẻ.
Nhờ vậy, nguyên lý xếp chồng không chỉ là một công cụ toán học mà còn là nền tảng tư duy giúp sinh viên, kỹ sư và nhà nghiên cứu hiểu sâu và làm chủ hệ thống điện – điện tử và cơ học hiện đại.
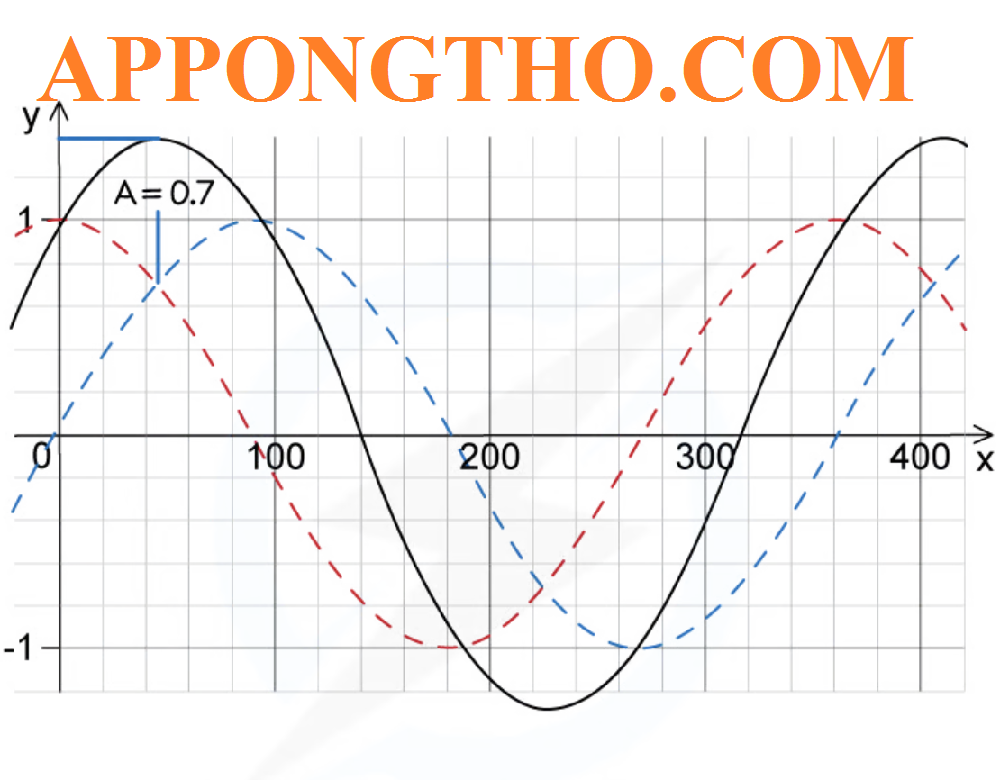
Nguyên lý xếp chồng là gì?
Nguyên lý xếp chồng (tiếng Anh: Superposition Principle) là một nguyên lý cơ bản trong nhiều lĩnh vực của khoa học và kỹ thuật, đặc biệt trong:
Vật lý (điện, sóng, cơ học),
Toán học tuyến tính,
Mạch điện và hệ thống điều khiển.
Nguyên lý xếp chồng phát biểu rằng: Nếu một hệ thống tuyến tính chịu tác động của nhiều nguồn tác động đồng thời, thì phản ứng tổng thể của hệ thống bằng tổng của các phản ứng riêng biệt khi từng nguồn tác động hoạt động một mình.
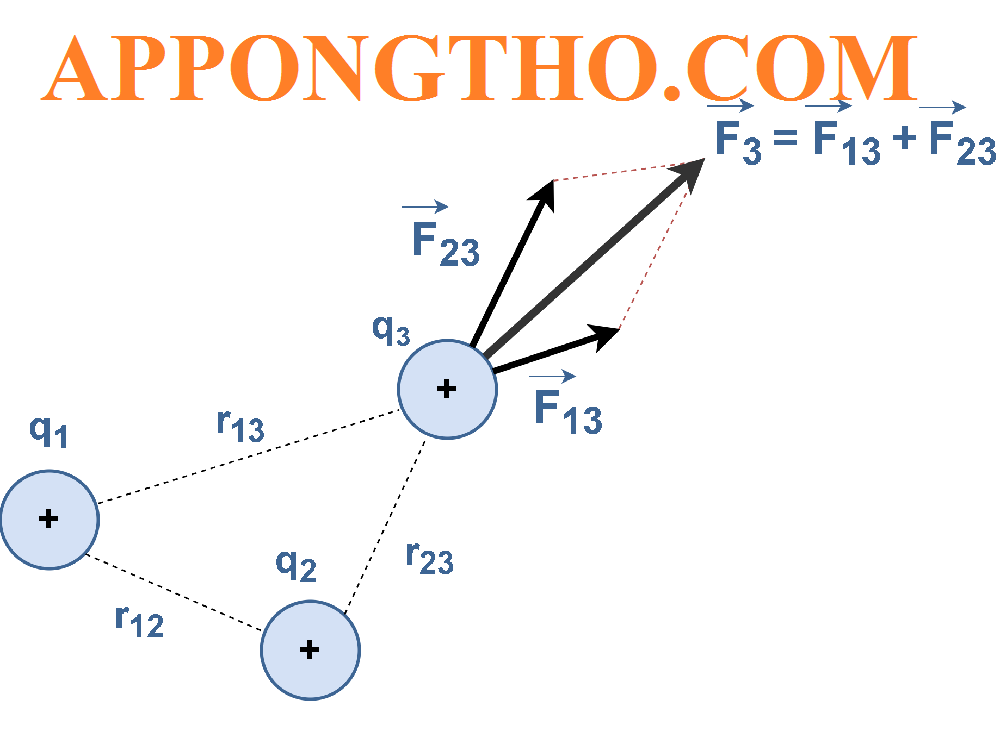
Nguyên lý xếp chồng lý thuyết mạch
Nguyên lý xếp chồng trong lý thuyết mạch điện phát biểu rằng: Trong một mạch điện tuyến tính chứa nhiều nguồn độc lập (nguồn điện áp hoặc dòng điện), dòng điện hoặc điện áp tại bất kỳ phần tử nào trong mạch bằng tổng đại số của các dòng điện hoặc điện áp do từng nguồn gây ra riêng lẻ khi các nguồn còn lại bị thay thế bởi trở kháng bên trong của chúng.
Bước 1: Chọn một nguồn độc lập, giữ nguyên nó.
Bước 2: Vô hiệu hóa các nguồn khác:
Bước 3: Phân tích mạch và tính đại lượng cần tìm (dòng, áp…).
Bước 4: Lặp lại với từng nguồn, sau đó cộng đại số tất cả kết quả.
Hệ thống mạch tuyến tính (R, L, C, nguồn độc lập hoặc phụ thuộc tuyến tính).
Không áp dụng cho mạch chứa thành phần phi tuyến (như diode, transistor trong vùng phi tuyến).
Trong cả mạch điện DC và AC (phân tích dòng điện, điện áp, công suất), đặc biệt hiệu quả với mạch điện xoay chiều tuyến tính.
Một mạch có hai nguồn điện áp: V1=10VV_1 = 10V, V2=5VV_2 = 5V.
Áp dụng nguyên lý xếp chồng, bạn sẽ:
Tính dòng hoặc áp khi chỉ có V1V_1 (và thay V2V_2 bằng dây dẫn).
Tính khi chỉ có V2V_2 (thay V1V_1 bằng dây dẫn).
Cộng kết quả lại để ra đáp số cuối cùng.

Phương pháp xếp chồng dòng điện
Phương pháp xếp chồng dòng điện là kỹ thuật phân tích mạch tuyến tính có nhiều nguồn độc lập, trong đó dòng điện qua một nhánh bất kỳ được tính bằng tổng đại số của các dòng điện do từng nguồn độc lập gây ra khi các nguồn còn lại bị vô hiệu hóa.
Bao gồm các nguồn điện áp và nguồn dòng điện độc lập.
Giữ lại 1 nguồn đang xét, vô hiệu hóa các nguồn còn lại:
Dùng các phương pháp phân tích như KVL, KCL, định luật Ohm, hoặc phân tích nút/mesh để tính dòng điện qua nhánh cần tìm.
Thực hiện tương tự cho từng nguồn còn lại.
Dòng điện tổng tại nhánh cần tìm là tổng đại số của các dòng riêng biệt (chú ý dấu “+” hay “–” tùy theo chiều dòng).
Chỉ áp dụng cho mạch tuyến tính (chứa R, L, C, nguồn tuyến tính).
Không dùng được cho mạch có phần tử phi tuyến (diode, transistor…).
Có thể áp dụng cho cả mạch DC và AC (phức) – trong AC, dùng số phức (dạng cực hoặc hình chữ nhật).
Một điện trở R = 5Ω,
Hai nguồn điện áp:
Đặt ở hai phía của điện trở.
Bạn sẽ:
1. Tắt V2 chỉ xét V1:
2. Tắt V1 chỉ xét V2:
3. Cộng lại:
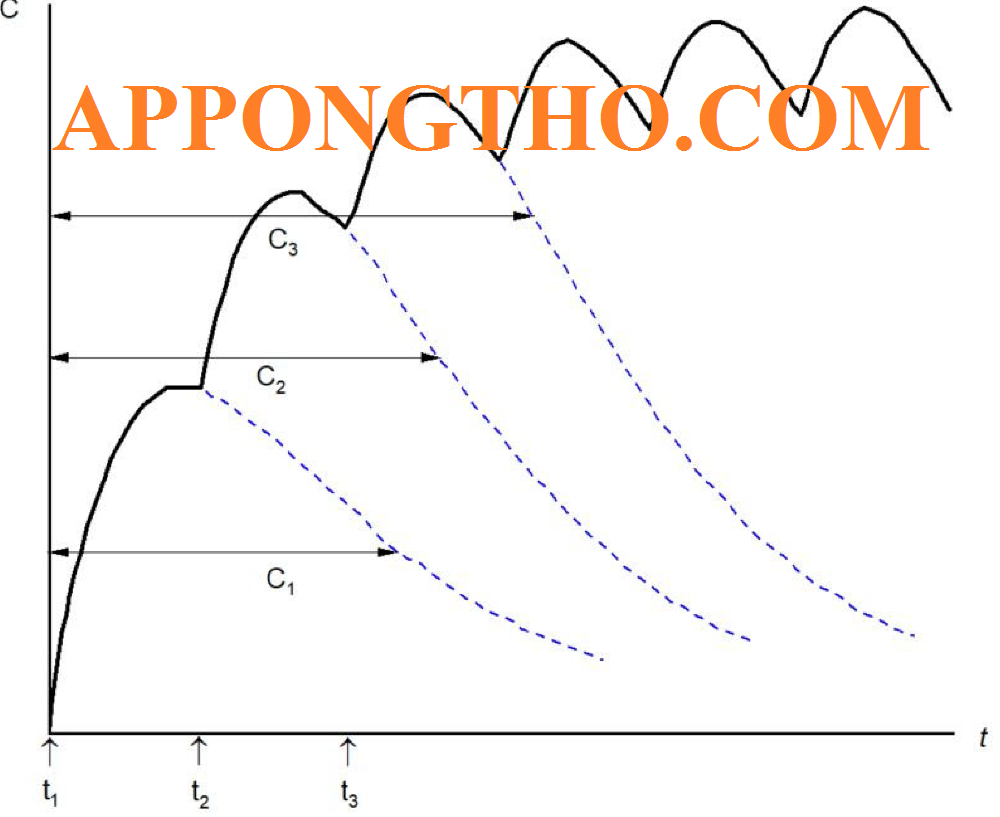
Các ứng dụng nguyên lý xếp chồng
Nguyên lý xếp chồng (Superposition Principle) có rất nhiều ứng dụng quan trọng trong phân tích, thiết kế và kiểm tra mạch điện.
Dưới đây là các ứng dụng cụ thể và phổ biến nhất:
Ứng dụng phổ biến nhất của nguyên lý xếp chồng là trong mạch có nhiều nguồn độc lập (nguồn điện áp hoặc dòng điện).
Thay vì phân tích toàn bộ mạch phức tạp cùng lúc, ta phân tích từng nguồn riêng biệt rồi cộng lại kết quả.
Rất hiệu quả khi tính:
Trong mạch điện xoay chiều tuyến tính, nguyên lý xếp chồng áp dụng tương tự như mạch DC.
Dùng đại lượng số phức (biểu diễn điện áp và dòng ở dạng pha).
Dễ dàng tính ảnh hưởng của từng nguồn xoay chiều với biên độ và pha khác nhau.
Trong các hệ thống điều khiển tuyến tính (ví dụ: mạch khuếch đại, servo…), nguyên lý xếp chồng giúp tách biệt ảnh hưởng của:
Dùng để xác định hiệu ứng riêng biệt của tín hiệu mong muốn và tín hiệu nhiễu trong các mạch thu/phát sóng, truyền dẫn…
Cho phép đánh giá mức ảnh hưởng của từng thành phần.
Trong xử lý tín hiệu, lý thuyết hệ thống tuyến tính dùng nguyên lý xếp chồng để xây dựng đáp ứng đầu ra từ nhiều tín hiệu vào khác nhau.
Ứng dụng trong phân tích biến đổi Laplace, Fourier, và các mạch lọc.
Trong các phần mềm như Multisim, LTSpice, Proteus…, nguyên lý xếp chồng giúp mô phỏng riêng từng nguồn để so sánh và kiểm chứng.
Hữu ích khi kiểm tra ảnh hưởng lỗi hoặc nguồn phụ.
Là phương pháp nền tảng trong giáo trình điện – điện tử đại cương.
Giúp người học hiểu rõ từng thành phần và ảnh hưởng của nguồn đến hệ thống.
Bài tập nguyên lý xếp chồng
Dưới đây là 4 bài tập nguyên lý xếp chồng (có lời giải chi tiết) để bạn luyện tập cách áp dụng vào phân tích dòng điện, điện áp trong mạch:
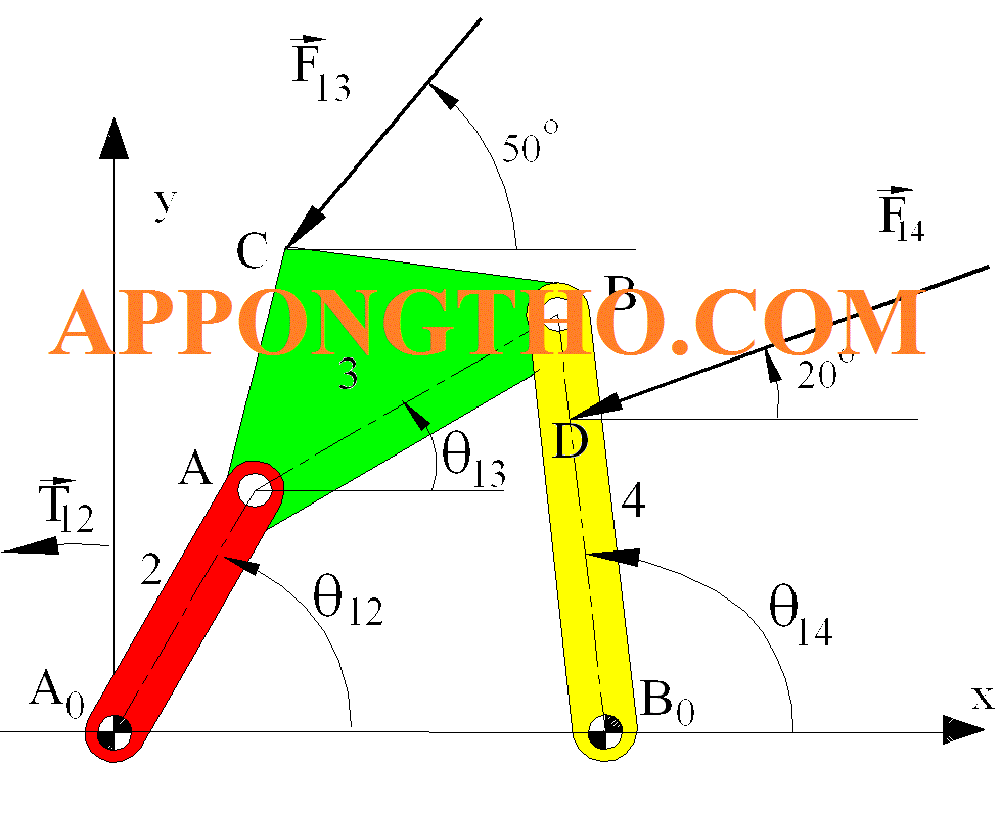
Đề bài: Một vật thể chịu tác dụng của ba lực đồng phẳng: có độ lớn 10 N hướng theo trục x dương, có độ lớn 15 N hướng theo trục y dương, và có độ lớn 20 N hợp với trục x dương một góc .
Xác định hợp lực tác dụng lên vật thể.
Hướng dẫn:
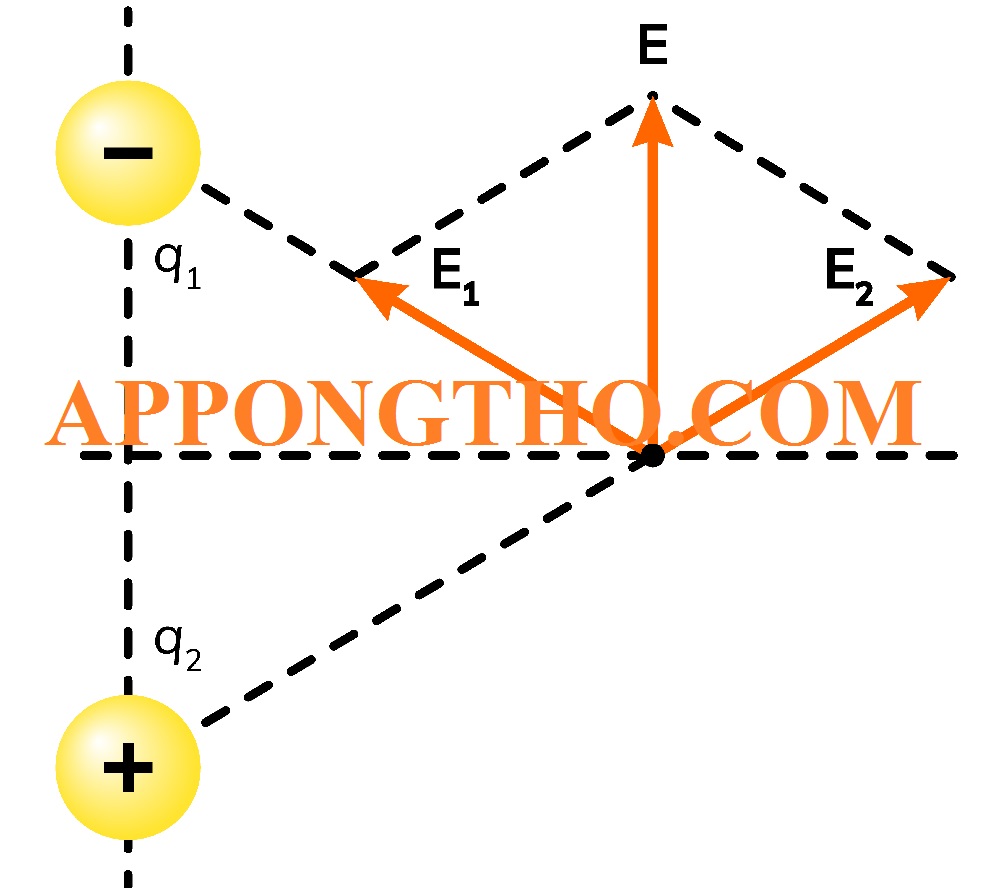
Đề bài: Cho hai điện tích điểm C đặt tại A(0, 3 cm) và C đặt tại B(4 cm, 0) trong mặt phẳng Oxy.
Xác định cường độ điện trường tổng hợp tại gốc tọa độ O(0, 0).
Hướng dẫn:
Đề bài: Một con lắc lò xo dao động điều hòa dưới tác dụng của một lực kéo về. Giả sử có thêm một lực ngoại tác không đổi tác dụng vào vật.
Mô tả sự thay đổi của vị trí cân bằng và biên độ dao động của vật dựa trên nguyên lý xếp chồng.
Hướng dẫn:
Đề bài: Một tấm kim loại phẳng có hai nguồn nhiệt điểm đặt tại các vị trí khác nhau. Nguồn nhiệt 1 tạo ra một sự tăng nhiệt độ tại một điểm (x, y) trên tấm kim loại, và nguồn nhiệt 2 tạo ra sự tăng nhiệt độ tại điểm đó.
Hãy sử dụng nguyên lý xếp chồng để xác định sự tăng nhiệt độ tổng cộng tại điểm (x, y) khi cả hai nguồn nhiệt cùng hoạt động, giả sử không có tương tác nhiệt phức tạp giữa các nguồn.
Hướng dẫn:
Dưới đây là các bước cơ bản để giải một bài tập mạch điện bằng phương pháp dòng điện vòng, cùng với một ví dụ minh họa:
Các bước giải bài tập mạch điện bằng phương pháp dòng điện vòng:
Đối với mỗi vòng, tổng đại số các sụt áp trên các phần tử trong vòng đó phải bằng tổng đại số các nguồn điện áp trong vòng đó.
Nếu một phần tử nằm trên biên giới giữa hai vòng, sụt áp trên phần tử đó sẽ phụ thuộc vào cả hai dòng điện vòng đi qua nó.
Ví dụ, nếu nằm giữa vòng và vòng , và dòng đi qua theo chiều dương của vòng , còn dòng đi qua theo chiều ngược lại, thì sụt áp trên trong phương trình của vòng sẽ là .
Sau khi có các dòng điện vòng, bạn có thể dễ dàng tính toán dòng điện qua bất kỳ nhánh nào trong mạch (bằng cách cộng hoặc trừ các dòng điện vòng đi qua nhánh đó) hoặc điện áp trên bất kỳ phần tử nào.
Hãy xét mạch điện đơn giản sau:
R1
+----/\/\/----+
| |
Vs1 R2
| |
+----/\/\/----+
| |
R3 Vs2
| |
+-------------+
Giả sử các giá trị:
Yêu cầu: Tìm dòng điện qua .
Giải:
Chúng ta có 2 vòng độc lập. Hãy chọn chiều dòng điện vòng theo chiều kim đồng hồ cho cả hai vòng.
Vòng 1: Chứa , , . Dòng điện vòng là .
Vòng 2: Chứa , , . Dòng điện vòng là .
R1 (I1)
+----/\/\/----+
| |
Vs1 R2 (I1-I2)
| |
+----/\/\/----+
| |
R3 (I2) Vs2
| |
+-------------+
Lưu ý: Dòng qua R2 là I1 – I2 nếu ta xét từ góc độ I1, hoặc I2 – I1 nếu ta xét từ góc độ I2.
Đối với Vòng 1:
Đi qua . Dòng đi xuống, dòng đi lên. Vậy dòng tổng qua theo chiều là . Sụt áp là .
Phương trình KVL cho Vòng 1: (1)
Đối với Vòng 2:
Đi qua từ dương sang âm: Phương trình KVL cho Vòng 2: (2)
Bước 3: Giải hệ phương trình.
Bạn có thể giải hệ này bằng phương pháp thế, phương pháp cộng đại số, hoặc dùng ma trận.
Nhân phương trình (1) với 4 và phương trình (2) với 3:
Bước 4: Tính toán đại lượng cần tìm.
Dấu âm cho thấy dòng điện thực tế qua có chiều ngược lại so với chiều chúng ta giả định (tức là hướng lên).
Vậy dòng điện qua có độ lớn là và hướng lên.
Phương pháp điện thế nút (Node Voltage Method) là một phương pháp phân tích mạch điện rất phổ biến trong kỹ thuật điện, dùng để tính toán điện áp tại các nút của mạch điện dựa trên định luật Kirchhoff về dòng điện (KCL – Kirchhoff’s Current Law).
Phương pháp điện thế nút dựa vào Định luật Kirchhoff dòng điện (KCL), nói rằng:
“Tổng dòng điện đi vào một nút bằng tổng dòng điện đi ra khỏi nút.”
Gán điện áp bằng 0 cho nút này. Tất cả các điện thế nút còn lại sẽ được tính so với nút gốc.
Viết phương trình dòng điện ra khỏi hoặc vào nút theo điện áp nút và định luật Ohm:
Thường sử dụng đại số tuyến tính để giải hệ n−1n-1 phương trình (do đã chọn 1 nút làm đất).
Cho mạch gồm ba nút:
Nút 0 là đất.
Hai nút còn lại là V1V_1 và V2V_2, nối với nhau qua điện trở và có một nguồn dòng.
Mạch:
Áp dụng KCL tại V1V_1 và V2V_2:
Tại V1V_1: V1R3+V1−V2R1=0\frac{V_1}{R_3} + \frac{V_1 – V_2}{R_1} = 0
Tại V2V_2: V2−V1R1+V2R2=I\frac{V_2 – V_1}{R_1} + \frac{V_2}{R_2} = I
Giải hệ này sẽ ra giá trị V1V_1, V2V_2.
Rất hiệu quả với mạch có nhiều nhánh và ít nút.
Phù hợp khi trong mạch có nhiều nguồn dòng.
Dễ lập trình và ứng dụng trong phần mềm mô phỏng như SPICE.
Phát biểu định lý Thevenin: “Bất kỳ một mạch điện tuyến tính hai cực A–B (gồm các nguồn điện và điện trở) đều có thể được thay thế bằng một mạch tương đương gồm một nguồn điện áp lý tưởng mắc nối tiếp với một điện trở Rth.”
1. VthV_{th} – Điện áp Thevenin:
2. RthR_{th} – Điện trở Thevenin:
Là điện trở tương đương nhìn từ hai đầu A–B khi:
Đơn giản hóa mạch điện để dễ tính toán.
Phân tích mạch phức tạp khi tải thay đổi.
Tối ưu công suất truyền vào tải (đi kèm với định lý công suất cực đại).
Mạch có:
Nguồn điện 12V nối tiếp với điện trở 4Ω.
Đầu ra là hai cực A–B sau điện trở đó.
👉 Mạch Thevenin tương đương:
Vth=12VV_{th} = 12V
Rth=4ΩR_{th} = 4Ω
Định lý Thevenin chỉ áp dụng cho mạch tuyến tính (chứa R, L, C, nguồn tuyến tính).
Không áp dụng cho mạch phi tuyến (ví dụ: diode, transistor mà không tuyến tính hóa).
(FAQ) Hỏi đáp về nguyên lý xếp chồng
Dưới đây là những câu hỏi và trả lời cụ thể về nguyên lý xếp cần có thể bạn đang cần:
Nguyên lý xếp chồng được áp dụng chủ yếu trong các hệ tuyến tính của vật lý và kỹ thuật như mạch điện, cơ học, điện từ, sóng và điều khiển tự động.
Mạch điện tuyến tính
Cơ học kết cấu
Trường điện – từ
Sóng âm và ánh sáng
Hệ điều khiển
Tĩnh điện và động học
→ Đây là một nguyên lý nền tảng giúp mô tả và tính toán hệ thống phức tạp bằng cách cộng tác động riêng rẽ.
Trong cơ học, nguyên lý xếp chồng cho rằng biến dạng tổng hợp tại một điểm là tổng các biến dạng do từng tải trọng riêng biệt gây ra.
Dùng trong kết cấu dầm
Tính ứng suất, biến dạng
Hệ vật liệu đàn hồi
Hệ chịu nhiều lực cùng lúc
Giải bài toán từng bước
Kết quả tuyến tính
→ Giúp kỹ sư dự đoán ứng xử của kết cấu phức tạp bằng cách cộng dồn từng ảnh hưởng đơn lẻ.
Trong điện trường, nguyên lý xếp chồng nói rằng tổng điện trường tại một điểm do nhiều nguồn gây ra bằng tổng vector của từng điện trường do mỗi nguồn tạo ra.
Điện tích điểm
Tổng vector E
Dùng định luật Coulomb
Tính điện trường tổng
Cần hệ tọa độ
Đúng với trường tuyến tính
→ Đây là công cụ không thể thiếu để phân tích điện trường phức tạp do nhiều điện tích gây ra.
Nguyên lý xếp chồng là một quy luật cho phép cộng các ảnh hưởng riêng biệt từ từng yếu tố gây ra để tính ảnh hưởng tổng hợp trong hệ tuyến tính.
Áp dụng rộng rãi
Mạch, sóng, điện trường
Tuyến tính là điều kiện
Giải bài toán từng phần
Đơn giản hóa tính toán
Phân tích hệ phức tạp
→ Đây là công cụ lý thuyết nền tảng trong vật lý hiện đại để phân tích các hiện tượng đa nguồn.
Trong kỹ thuật, nguyên lý xếp chồng giúp phân tích các hệ có nhiều nguồn tác động bằng cách tách rời và tính riêng từng phần.
Tính mạch điện
Phân tích kết cấu
Điều khiển tự động
Hệ thống rung động
Thiết kế anten
Phát triển phần mềm mô phỏng
→ Nhờ đó, kỹ sư có thể xử lý các hệ thống phức tạp một cách chính xác và linh hoạt hơn.
Ưu điểm lớn nhất là khả năng đơn giản hóa hệ thống tuyến tính bằng cách xử lý từng nguồn một cách riêng rẽ.
Tính toán nhanh
Phân tích dễ
Tách biệt từng nguồn
Tránh nhầm lẫn
Phù hợp với mô phỏng
Tối ưu hóa thiết kế
→ Đây là một phương pháp giúp tiết kiệm thời gian và nâng cao độ chính xác trong phân tích hệ thống.
Nguyên lý xếp chồng không áp dụng cho các hệ phi tuyến, tức là khi đầu ra không tỷ lệ tuyến tính với đầu vào.
Mạch diode
Transistor hoạt động phi tuyến
Hệ vật liệu phi tuyến
Sóng có biên độ lớn
Tác động phụ thuộc nhau
Không thỏa điều kiện siêu vị
→ Việc sử dụng nguyên lý này trong hệ phi tuyến sẽ dẫn đến sai số và kết quả không chính xác.
Hai tên gọi này thực chất là một, đều đề cập đến cùng một nguyên lý trong phân tích hệ tuyến tính.
Tên gọi khác nhau
Nghĩa giống nhau
Cùng áp dụng cho hệ tuyến tính
Cùng dùng trong vật lý
Hay gặp trong mạch điện
Phân tích tương tự
→ Do đó, bạn có thể dùng từ nào cũng được tùy theo văn cảnh nhưng nội dung không đổi.
Ví dụ điển hình là mạch điện có nhiều nguồn áp và dòng; ta tính dòng qua điện trở bằng cách xét từng nguồn riêng biệt và cộng kết quả.
Mạch điện nhiều nguồn
Dầm chịu nhiều lực
Trường điện do nhiều điện tích
Sóng giao thoa âm
Ánh sáng chồng nhau
Hệ dao động cưỡng bức
→ Những ứng dụng này đều chứng minh rõ cách nguyên lý xếp chồng giúp ta giải quyết vấn đề từng phần.
Trong tĩnh điện, nguyên lý xếp chồng dùng để tính tổng điện thế hoặc điện trường do nhiều điện tích điểm gây ra.
Từng điện tích riêng
Tổng điện trường vector
Dùng trong hệ nhiều điện tích
Cần biết vị trí điểm khảo sát
Liên quan Coulomb
Ứng dụng tính lực tương tác
→ Nguyên lý này giúp tính nhanh trường tĩnh điện phức tạp bằng phương pháp cộng đơn giản.
Trong mạch xoay chiều, nguyên lý xếp chồng áp dụng được bằng cách dùng số phức (phazor) để cộng từng đáp ứng.
Dùng đại số phức
Nguồn điện hình sin
Tách từng nguồn riêng
Dễ cộng hưởng
Có thể dùng ma trận
Cộng đại số phasor
→ Đây là công cụ mạnh mẽ trong phân tích hệ AC với nhiều tần số và nguồn sin.
Khi hai hay nhiều sóng gặp nhau, tổng biên độ tại một điểm là tổng đại số của từng sóng, gọi là giao thoa sóng.
Sóng âm
Sóng nước
Giao thoa ánh sáng
Tạo cực đại – cực tiểu
Biên độ cộng lại
Điều kiện pha quan trọng
→ Hiện tượng giao thoa là minh chứng nổi bật của nguyên lý xếp chồng trong vật lý sóng.
Trong quang học, nguyên lý xếp chồng giải thích hiện tượng giao thoa và nhiễu xạ ánh sáng khi nhiều tia sáng chồng lên nhau.
Giao thoa ánh sáng
Nhiễu xạ
Sóng ánh sáng tuyến tính
Thí nghiệm khe Young
Biên độ cộng đại số
Ứng dụng trong laser
→ Đây là cơ sở lý thuyết giúp giải thích tính chất sóng của ánh sáng trong quang học sóng.
Trong động lực học, nguyên lý xếp chồng giúp phân tích chuyển động phức tạp bằng cách cộng chuyển động riêng do từng lực gây ra.
Chuyển động tuyến tính
Phân tích dao động
Nhiều lực tác động
Dễ giải phương trình
Dùng trong điều khiển học
Áp dụng cho hệ đàn hồi
→ Nhờ đó, ta dễ dàng mô hình hóa và phân tích các chuyển động trong hệ đa lực.
Bài tập thường yêu cầu xác định điện áp hoặc dòng qua một phần tử khi mạch có nhiều nguồn, bằng cách xét riêng từng nguồn.
Mạch RLC nhiều nguồn
Dầm chịu nhiều tải
Trường E do nhiều điện tích
Giao thoa sóng
Điều khiển tuyến tính
Kết cấu hỗn hợp
→ Các bài tập này rèn luyện khả năng tách biệt và tổng hợp các tác động tuyến tính một cách hệ thống.
Hạn chế lớn nhất là không áp dụng được cho hệ phi tuyến, vì đáp ứng không tỷ lệ với đầu vào.
Không dùng với diode
Sai với mạch transistor
Không áp dụng sóng lớn
Không tính hiệu ứng phụ
Hạn chế vật liệu phi tuyến
Không đúng nếu có bão hòa
→ Vì vậy, nguyên lý này chỉ hữu ích khi hệ thống tuân theo các đặc tính tuyến tính nghiêm ngặt.
Tóm lại, nguyên lý xếp chồng là một nguyên tắc then chốt trong phân tích các hệ tuyến tính, đặc biệt là mạch điện có nhiều nguồn tác động đồng thời.
Bằng cách tách riêng từng nguồn và phân tích ảnh hưởng độc lập của chúng, ta có thể giải bài toán một cách đơn giản và hiệu quả hơn.
Khi kết hợp với các phương pháp khác như dòng điện vòng, điện thế nút, và các định lý nổi tiếng như Thevenin hay Norton, nguyên lý xếp chồng trở thành một phần không thể thiếu trong kho công cụ giải tích mạch điện.
Tuy nhiên, điều quan trọng là phải nhận biết được giới hạn của nguyên lý này – nó chỉ đúng trong các hệ tuyến tính và không áp dụng cho các thành phần phi tuyến như diode, transistor ở vùng hoạt động không tuyến tính.
Với sự hiểu biết sâu sắc và vận dụng đúng đắn, nguyên lý xếp chồng sẽ giúp người học và kỹ sư làm chủ những hệ thống kỹ thuật phức tạp, góp phần vào việc thiết kế và tối ưu các thiết bị điện – điện tử hiện đại ngày nay.